5 equações que mudaram o mundo, explicadas por um físico
Marcelo Lapola exalta o poder das fórmulas matemáticas para descrever as leis da natureza e lista as principais que mudaram nossa compreensão da realidade e do Universo
Quando o físico norte-americano Richard Feynman foi apresentado ao também físico britânico Paul Dirac, este logo de cara lhe perguntou: “diga-me, Sr. Feynman, o senhor tem uma equação com o seu nome?”
Àquela altura, Feynman não tinha especificamente uma fórmula matemática batizada em sua homenagem. Já Dirac vivia o auge da fama justamente por ter descoberto uma bela expressão matemática que descrevia os elétrons, a tal da “Equação de Dirac”, da teoria quântica de campos — conceito que o próprio Feynman ajudara a criar.
Anos antes, ao recusar o convite para ser presidente do recém-criado estado de Israel, Einstein disse que não gostaria de abandonar seu estado ininterrupto de contemplação da natureza e suas leis. “A política serve ao momento presente. Uma equação é para a eternidade”, cravou.
Você consegue imaginar o que é ter uma equação com o seu nome? Descobrir uma lei fundamental da natureza, como fez Newton, e estabelecê-la numa linda e imutável fórmula matemática?
A busca por fama instantânea, seguidores, visibilidade e relevância nesses nossos dias parece ser menor quando comparadas às equações, que tornam eternos os feitos de homens e mulheres da ciência neste nosso mundo.
E essa aventura que começou a milhares de anos, parece não ter fim. Há sempre novas equações a serem descobertas que poderão nos levar a outro patamar de progresso e entendimento do Universo.
A lista de fórmulas importantes é enorme. A seguir, conheça cinco destas equações que mudaram o mundo:
1. Equivalência massa-energia
Equivalência massa-energia — Foto: Reprodução
Nada mais justo do que iniciar essa lista com a equação mais famosa de todas. Publicada pela primeira vez em 1905 por Albert Einstein, a equação que nos diz que matéria é energia foi descoberta como consequência da Teoria da Relatividade Especial.
Na equação E=m.c², E representa a energia , m é a massa (quantidade de matéria de um corpo) e c é a velocidade da luz (cerca de 300 mil quilômetros por segundo).
Esta fórmula simples nos permitiu entender profundamente como as estrelas e o universo funcionam, nos fez compreender ainda mais os núcleos atômicos e permitiu, entre outras coisas, a construção de aceleradores de partículas (como o LHC) para sondarmos a natureza quântica do mundo subatômico.
2. Teorema de Pitágoras
Tópico:
SOBRE A ATIVIDADE
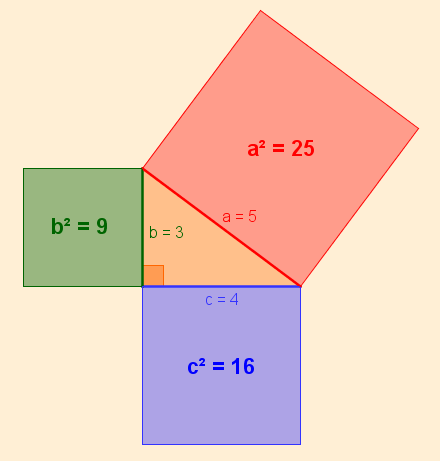
Teorema de Pitágoras — Foto: Reprodução
Uma das primeiras regras da trigonometria que a gente aprende na escola é essa relação entre os lados de um triângulo retângulo. Aprendemos a repetir: “a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa”.
Em palavras mais simples, quer dizer que o comprimento de cada um dos dois lados menores do triângulo, elevados ao quadrado e somados, é igual ao comprimento do lado maior do triângulo ao quadrado. Essa relação matemática é conhecida há pelo menos 3,7 mil anos, desde o tempo dos babilônios. Mas a versão que conhecemos da equação é creditada ao filósofo e matemático grego Pitágoras (que viveu no século 6 a.C.).
O uso do Teorema de Pitágoras é imenso: ele está presente na construção, na navegação, no mapeamento, na triangulação de sinais de satélites de comunicação, além de ter ajudado muito a expandir o próprio conceito dos números.
3. Segunda Lei de Newton
De acordo com a segunda lei de Newton, a força resultante sobre um corpo é igual ao produto da massa pela aceleração.

Segunda Lei de Newton — Foto: Reprodução
“A força resultante que atua sobre um corpo é proporcional ao produto da massa pela aceleração por ele adquirida”.
Essa relação pode ser descrita com a equação:
Fr = m . a
sendo:
Fr – Força resultante;
m – massa;
a – aceleração.
De acordo com essa Lei, para que se mude o estado de movimento de um objeto, é necessário exercer uma força sobre ele que dependerá da massa que ele possui. A aceleração, que é definida como a variação da velocidade com o tempo, terá o mesmo sentido da força aplicada, conforme mostra a figura abaixo:

Ao aplicar uma força sobre um objeto, imprimimos sobre ele uma aceleração que será dependente de sua massa
Podemos ver a partir da figura que, ao aplicar uma força de 2N sobre um objeto, ele adquirirá uma aceleração maior quando a massa for 0,5 kg e uma pequena aceleração quando a massa for 4 kg. Isso significa que quanto maior a massa de um corpo, maior precisa ser a força aplicada para que se altere seu estado de movimento.
Sendo a inércia definida como a resistência de um corpo para alterar seu estado de movimento, podemos dizer que a segunda lei de Newton também define a massa como a medida da inércia de um corpo.
A força é uma grandeza vetorial, pois, precisa ser caracterizada por módulo, direção e sentido. A unidade no Sistema Internacional é o Newton, N, que representa kg m/s2.
A segunda Lei de Newton também é chamada de princípio fundamental da dinâmica, pois, é a partir dela que se define a Força como uma grandeza necessária para se vencer a inércia de um corpo.
Uma pequena e simples, porém, poderosa expressão matemática. Força (F) igual a massa (m) multiplicada pela aceleração (a). O conceito de força como causa para o movimento acelerado dos corpos surgiu das ideias de Sir Isaac Newton, publicadas pela primeira vez em 1687.
Podemos dizer que a massa de um corpo é justamente a quantidade de matéria que ele tem. E a aceleração é a taxa de variação da velocidade (o acelerador de um carro não tem esse nome por acaso!).
A matemática por trás disso é bem simples. Se duplicar a força, duplica a aceleração. Mas, se duplicar a massa, reduz a aceleração pela metade.
Bem, foi a mecânica newtoniana, embasada por suas três leis, que possibilitou a Revolução Industrial no século 18 na Inglaterra, fez a engenharia progredir, possibilitou a construção de máquinas e veículos, levou o homem à Lua, colocou satélites em órbita e muito muito mais.
4. Lei da Gravitação Universal

Lei da Gravitação Universal — Foto: Reprodução
Como se lê:
O que diz?
Por que é importante?
Quais foram as consequências?
Referências:
- 17 equações que mudaram o mundo - Ian Stewart
Links para este artigo:
Aos 23 anos, depois de ver uma maçã cair, com uma simples pergunta, Newton mudou o rumo da história: “Se uma maçã cai, a lua também cai?”
Uma extensão importante das leis do movimento é a Lei da Gravitação Universal. Até então se acreditava nas ideias de Aristóteles de que as leis naturais que valiam para os céus eram diferentes das leis da natureza na Terra. Foi Newton quem as unificou e mostrou que a mesma força que faz qualquer objeto cair na superfície da Terra é a que mantém a Lua, planetas, estrelas e galáxias em órbita.
Na fórmula, F é a força da gravidade, m1 e m2 são as massas de dois objetos e d é a distância entre eles. G é uma constante fundamental cujo valor foi descoberto através da experimentação. Esses conceitos têm sido usadospara entender muitos sistemas físicos desde então, incluindo o movimento dos planetas no Sistema Solar e os meios de viajar entre eles usando foguetes e sondas espaciais.
5. Equações de Maxwell
POR QUE AS EQUAÇÕES DE MAXWELL SÃO TÃO IMPORTANTES E O QUE ELAS REALMENTE SIGNIFICAM?

Hoje, a principal equação da física é a equivalência de energia e massa, a E = mc². Essa equação é tão famosa que até mesmo um leigo a encontrou ou a viu em algum lugar pelo menos uma vez na vida. A equivalência da energia e massa pertence à teoria da relatividade especial, idealizada por Albert Einstein em 1905. Mas qual é a origem da relatividade especial? A resposta é eletricidade e magnetismo. Sim! Você leu certo. As raízes da teoria da relatividade estão incorporadas nas quatro famosas equações da eletricidade e magnetismo, as Equações de Maxwell.

Equações de Maxwell — Foto: Reprodução
James Maxwell era um físico teórico que provou que Faraday estava certo. Faraday supôs que a luz é uma onda eletromagnética. Faraday não era um cientista teórico rigoroso, mas Maxwell era. Estas 4 equações não são formuladas por Maxwell. As duas primeiras equações são as leis de Gauss da eletricidade e do magnetismo respectivamente, a terceira equação é a lei de Faraday e a quarta é a lei circuita de Ampere com um termo de correção que foi introduzido por Maxwell. Então, por que elas são nomeadas em sua homenagem? A razão é que Maxwell reuniu essas equações independentes da eletricidade e do magnetismo e mostrou que ambos estão profundamente conectados.
As equações de Maxwell foram o ponto de virada na história da humanidade. Como Carl Sagan disse: “Elas tiveram um impacto maior na história humana do que quaisquer dez presidentes.” Vamos agora olhar para estas equações que mudam o jogo e o que elas realmente significam.
1. Lei de Gauss da Eletrostática

Significado da equação
A lei de Gauss da eletrostática nos diz três coisas importantes. Primeiro: pode existir uma carga elétrica independente no espaço. Isso significa que uma única carga positiva ou uma única carga negativa podem ter sua própria existência. Elas não precisam existir em pares. Segundo: O número de linhas de campo elétrico que sai de um volume é diretamente proporcional à carga contida nele. Terceiro: O campo elétrico, como o campo gravitacional, segue a lei do inverso do quadrado. Assim, a lei de Gauss é apenas outra versão da lei de Coulomb em eletrostática.
2. Lei de Gauss da magnetostática

Significado da Equação
Esta é a mais fácil das quatro equações de Maxwell. O significado desta equação é: monopólos magnéticos não existem na natureza. Então, se você cortar um ímã em duas partes, não terá pólos norte e sul separados. Em vez disso, você terá dois novos ímãs de barra, cada um com seu próprio par de pólos norte e sul. Se monopólos magnéticos forem descobertos, o lado direito da equação mudará.
3. Lei de Faraday

Significado da Equação
Se você estiver usando qualquer coisa que funcione com eletricidade, agradeça esta equação. Nada teria sido possível sem essa terceira equação, conhecida como a lei de Faraday. Essa equação é o arquiteto do mundo moderno. Diz, Um fluxo magnético em mudança através de um circuito fechado produzirá uma força eletromotriz nesse circuito. Uma declaração notável em si. Assim, você pode produzir um campo elétrico a partir do próprio ímã. Nenhuma outra equação capta o belo elo entre os dois campos diversos do que este. A equação de Faraday possibilitou a construção de solenoides, motores elétricos, geradores e transformadores.
4. Lei Circuita de Ampere

Significado da Equação
A lei de Ampere nos diz que um fio condutor atual produz um campo magnético que circunda o fio e é proporcional à quantidade de corrente que flui através do fio condutor. Bem, essa equação era um marco em si. Diz que todos os efeitos magnéticos são realmente causados pelas correntes, que nada mais são que partículas carregadas em movimento.
Outra coisa importante sobre esta lei é que ela é matematicamente incorreta na forma dada acima. Isso foi notado por Maxwell e ele acrescentou um novo termo à lei. Então a lei modificada de Ampere é:

O segundo termo do lado direito é a correção adicionada. Isso não apenas corrige a matemática da equação, mas também adiciona uma bela simetria às equações de Maxwell. A correção na verdade significa que podemos ter um campo magnético de um campo elétrico variável, exatamente oposto à terceira equação, que diz que o campo elétrico pode ser gerado a partir de um campo magnético variável.
Então agora você pode ver como essas equações são importantes para física. Essas 4 equações, juntamente com a equação da continuidade, são os blocos de construção de toda a eletrodinâmica.
Traduzido e Adaptado de: https://secretsofuniverse.in/2018/11/12/why-maxwells-equations-are-so-important-and-what-do-they-really-mean/?fbclid=IwAR1QLQqeqgL0J9z4IbAGoidFx5JQQSVD_IifgGr8k2yv8u4OmvSTtwvn8aA
O estudo dos campos de força, elétrico e magnético, descobertos por Faraday, Oersted e outros, carecia de uma sistematização matemática mais profunda. E isso foi feito por um prodígio da matemática em 1864. O escocês James Clerk Maxwell encontrou 20 equações descrevendo como eletricidade e magnetismo estavam inter-relacionados.
Mais tarde, estas equações foram resumidas em apenas quatro. E uma das importantes descobertas a partir da combinação dessas quatro equações é a equação das ondas eletromagnéticas. As equações de Maxwell estão por trás de todo avanço tecnológico na eletrônica e nas comunicações do nosso mundo moderno.
Há muitas outras equações tão importantes quanto estas listadas aqui, e novas sendo descobertas. A física e a matemática, usadas como ferramenta, são o que há de mais perfeito e duradouro para contemplarmos em nossa tão curta, tão passageira vida, diante da imensidão do espaço e do tempo.
Quer saber mais sobre estas e outras equações que mudaram a forma como compreendemos o Universo? Talvez você curta essas leituras:
17 Equações que Mudaram o Mundo, por Ian Stewart e George Schlesinger (Editora Zahar, 408 páginas | Impresso: R$ 77,90 • E-book: R$ 44,90)
/i.s3.glbimg.com/v1/AUTH_fde5cd494fb04473a83fa5fd57ad4542/internal_photos/bs/2022/l/p/ZMpv3eQ0AymFQutKvvdQ/thisisengineering-raeng-gzdrm7syq0g-unsplash.jpg)
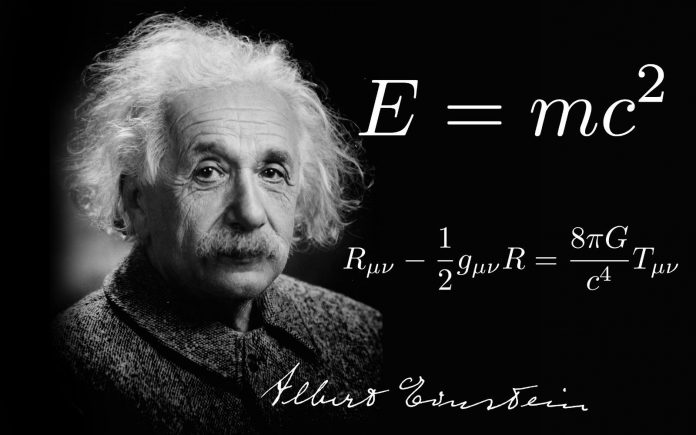
Comentários
Postar um comentário